Матеріали семінару-практикуму для вчителів математики навчальних закладів області, 

які працюють із математично обдарованими дітьми 

(на базі Білоцерківської СПМШ І-ІІІ ступенів № 16 ім. М.О.Кириленка)

(21.10.15)

Заняття №1

РОЗМИНКА, АБО ТРОХИ ЛОГІКИ НА УРОЦІ НЕ ЗАШКОДИТЬ

Корисно, ОСОБЛИВО У 5-8 КЛАСАХ  розв’язувати нескладні логічні задачі на уроці. Це сприятиме  формуванню в учнів вміння будувати ланцюжок міркувань, не сплутувати причину й наслідок, сприятиме зацікавленості їх математикою, покращить навчання, зокрема геометрії.

Такі задачі можуть бути використані вчителем на будь-якому етапі проведення уроку з будь-якої теми, у будь-якому класі, як з метою розвитку логічного мислення учнів, так і зняття втоми, підвищення інтересу до предмета.

Зверніть увагу дітей, що  обернене до правильного твердження не завжди є правильним! Якщо кіт має вуса, то не кожен вусатий є котом. Множина-наслідок ширша за множину-виток.

Задача 1. За добу до дощу кіт Петрика завжди чихає. Сьогодні він чхнув. Чи правда, що завтра піде дощ?

Відповідь: Невідомо (може кіт просто застудився).

Задача 2. Вчитель математики сказав: «Хто першим розв’яже цю задачу – отримує цукерку». Чи означає це, що учні, які  не  розв’яжуть першими цю задачу  не їстимуть цукерок? Відповідь обґрунтуйте.

Задача 3. Поставте між двома твердженнями знак наслідку.

1. Літак.   …    Літає.
2. Я зайшов у свій дім.    …    Я зайшов у свою квартиру.
3. Х² =1 … Х = 1.

У наступній задачі доцільно запропонувати учням зобразити відповідні множини (поясніть, що так роблять математики, а зображення називають діаграмами  Вена або кругами Ейлера).

Задача 4. Чи правильними є пропоновані твердження. Відповідь обґрунтуйте.

1. Всі кози їдять капусту.  Лада – коза. Тоді вона їсть капусту.
2. Всі кози їдять капусту.  Лада  їсть капусту. Тоді вона – коза.
3. Всі дерева мають листя. Всі кущі мають листя. Тоді всі кущі – дерева. 
4. Всі риби вміють плавати. Деякі коники – риби. Тоді деякі коники вміють плавати.
5. Всі мавпи полюбляють банани. Деякі діти полюбляють банани. Тоді деякі діти – мавпи.

Задачі логічного спрямування можуть сприяти розвитку в учнів уяви, особливо, якщо задіяти їх практичну діяльність.

Задача 5. Одна людина положила олівець на підлогу так, що жоден не зміг його перестрибнути. Поясніть як таке сталося.

Відповідь: Олівець положили попід стінкою.

Задача 6. Скільки кінців у двох палок? А в чотирьох із половиною?

Задача 7.  Стрічку розрізали на 10 частин. Скільки розрізів було зроблено?

Задача 8.  Круглий кекс із діркою посередині розрізають на 10 частин (на сектори). Скільки розрізів зроблено? Чому відповідь інша ніж у задачі №5?

Задача 9. На великому круглому торті зробили 10 прямолінійних розрізів так, що кожний розріз проходив через центр торта (від краю до краю). Скільки шматків вийшло?

Задача 10. Двоє людей зробили на двох квадратних тортах по два прямолінійних розрізи від краю до краю (кожен на своєму). Один отримав три куски, а другий – чотири. Як таке могло статися?

Задача 11. Як поділити круглий торт трьома прямолінійними розрізами на чотири, п’ять, шість, сім частин?

Задача 12. Якої форми має бути торт, щоб одним прямолінійним розрізом його можна було поділити на чотири частини?

Відповідь: Наприклад, у вигляді літери Ш.

 Задача 13. Як поділити одним розрізом круглий торт рівно навпіл?

Відповідь: Провести розріз через центр круга.

Задача 14. Як поділити одним розрізом прямокутний торт рівно навпіл?

Відповідь: Провести розріз через середину протилежних сторін; провести розріз вздовж діагоналі; провести розріз по довільній прямій, що проходить через точку перетину діагоналей. Порада. Щоб підвести учнів до останнього розв’язку, запропонуйте їм відповідними чином розрізати прямокутник і спробувати сумістити кусочки. Зауваження. Така практична робота підготує учнів до доведення у 7 класі ознаки паралельності двох прямих.

Задача 15. На прямокутний торт поклали (довільним чином) круглу шоколадку. Як розрізати торт на дві рівних частини так, щоб поділити й торт, і шоколадку навпіл?

Відповідь: Провести розріз через дві точки – центр круга та точку перетину діагоналей прямокутника.

Задача 16. Роздягаючись, Незнайка закидає під ліжко шкарпетки. Він має 12 червоних і 12 синіх шкарпеток. Скільки найменше шкарпеток йому потрібно витягти зранку з-під ліжка, щоб із них можна було скласти хоча б одну пару шкарпеток однакового кольору, якщо він робить це із заплющеним очима?

Відповідь: 3. Порада. Заплющте очі та уявіть себе Незнайкою: ось ви витягли одну шкарпетку, нехай вона буде синя; ось ви витягли другу, нехай вам не повезло й вона червона; ось ви витягаєте третю якогось кольору …  

Задача 17. А якщо у попередній задачі то будуть не шкарпетки, а штиблети?

Відповідь: 25.

Задачі логічного спрямування допоможуть навчити учнів виділяти логічні кроки розв’язування.

Задача 18. У Віні-Пуха та П’ятачка в кишенях однакова кількість монет. Скільки монет П’ятачок повинен дати Віні-Пуху, щоб в нього стало на 4 монети більше ?

Розв’язання

Нехай у П’ятачка та Віні-Пуха було по N монет.

1. П’ятачок дає Віні-Пуху 1 монету. Тоді у нього буде N 1 монета, а у Віні-Пуха N + 1 монета, тобто на 2 монети більше.
2. П’ятачок дає Віні–Пуху ще одну монету. Тоді у нього буде N – 1 – 1 = N 2 монети, а у Віні-Пуха N + 1 + 1 = N + 2 монети, тобто на 4 монети більше.

Відповідь: П’ятачок повинен дати дві монети.

Питання «на засипку». Скільки монет П’ятачок повинен дати Віні-Пуху, щоб в нього стало на 5 монети більше ?

Задача 19. На заміщення посади радника одного східного володаря претендували чотири мудреці. Щоб зробити остаточний вибір, претендентів перевірили на кмітливість.

Усім чотирьом зав’язали очі і, посадивши навколо столу, сказали: «На лобі кожного з вас поставили чорну або білу мітку, причому чорних більше, ніж білих». Потім у претендентів зняли пов’язки і кожен зміг побачити мітки, зроблені іншим. Той, хто визначить колір мітки на власному лобі, мав стати радником. Довго дивилися претенденти один на одного. Нарешті один сказав: «У мене на лобі чорна мітка». Відповідь виявилася правильною. Як він міркував?

Розв’язання

Мудрець здогадався, що всі мітки були чорними. А міркував він приблизно так.

1. Білою може бути лише одна мітка (інакше білих міток буде більще ніж чорних, або стільки, скільки чорних, а за умовою чорних міток більше).
2. Якщо на моєму лобі була б біла мітка, то троє інших претендентів легко здогадалися б, що в них чорні мітки, а вони мовчать. Висновок – у мене на лобі чорна мітка!

Відповідь: Мудрець здогадавсь, що всі мітки були чорними.

Задачі логічного характеру можуть навчити учнів  моделювати.

!!! Прямокутниками можна зображати не тільки мішки із морквою, а й будь-які величини, наприклад гроші.

Задача 20. Якщо взяти в мене з гаманця половину грошей і додати до них 1 грн., то вийде 25 грн. Скільки грошей у мене в гаманці?

Відповідь: 48 грн. Порада. Зобразіть гаманець у вигляді прямокутника. Розділять його навпіл. Домалюйте квадратик й впишіть у нього «1 грн.». Бачимо, що половина грошей у гаманці дорівнює 25 – 1 = 24 (грн.). Тоді в гаманці загалом  (грн.).

Задача 21. Половина моїх грошей та ще половина цієї половини, та ще 4 грн. – от і всі мої гроші. Скільки в мене грошей?

Відповідь: 16 грн. Порада. Зобразіть всі гроші прямокутником. Поділіть його на чотири рівні частини («цеглинки»). З малюнка маємо, що чотири «цеглинки» дорівнюють трьом  «цеглинкам» плюс 4 грн. Тоді одній «цеглинці» відповідають 4 грн. Усі гроші – то чотири «цеглинки», отже маємо загалом  (грн.).

Задача 22. Ліфт може перевозити одночасно або 12 дорослих, або 20 дітей. Скільки дітей можуть їхати в ліфті одночасно з дев’ятьма дорослими?

Відповідь: 5 дітей. Порада. Зауважимо, що числа 12 і 9 діляться на 3. Тоді змоделюємо умову так.

1. Зобразимо 12 дорослих блоками по три у вигляді квадратиків – їх чотири                          (мал. 3.5).
2. 20 =4, тобто кожному квадратику можна поставити у відповідність кружечок із п’ятьма дітьми.
3. Отже, маса трьох дорослих (один квадратик) дорівнює масі п’ятьох дітей (один кружечок).
4. Ліфт вміщає 12 дорослих - чотири квадратики. Якщо маємо дев’ять дорослих (три квадратики), то замість четвертого квадратика ліфт можна доповнити одним кружечок – п’ятьма дітьми.

Питання «на  засипку». Скільки дорослих можуть їхати в такому ліфті одночасно з 15 дітьми? Скільки дорослих може зайти до цього ліфта, якщо в ньому вже є 17 дітей? А якщо дітей буде 18? А у випадку 19 дітей?

Задача 23. Усі тварини в Бабусі, крім двох, - кози, усі, крім двох, – кішки, усі, крім двох, собаки, а всі інші – кури. Скільки курей в Бабусі? Скільки інших тварин в бабусі?

Відповідь: Немає курей, інших тварин – по одній; 2 курки і немає інших тварин.

Задачі логічного спрямування можна знайти у посібнику Апостолової Г.В., Бакал О.П. «Логічними стежинками математики».

І. ПОЧАТОК НАВЧАЛЬНОГО РОКУ – ЦЕ ПОВТОРЕННЯ. ВИКОРИСТАННЯ ОПОРНИХ СХЕМ У РОБОТІ

Важливо повторити основні опорні факти вивченого раніше. Як це зробити  найшвидше та ефективніше? Задійте зорову пам’ять учнів – створіть опорний конспект. (Приклад такого конспекту з геометрії «Пам’ятаємо з сьомого класу»,  ви знайдете на с. 4-5  посібника Г. Апостолової  «Геометрія в опорних схемах і малюнках. Робочий зошит учня 8 кл.»)

Це дозволить швидко повторити основні опорні  факти вивченого раніше (вчитель проговорює їх по малюнкам,  що має перед собою учень), акцентувати увагу учнів на основних опорних задачах, закріпити відповідні знання при розв’язуванні задач (якщо дозволити учням  дивитися в такий узагальнюючий конспект).

У подальшому можна вводити як «робочі» опорні конспекти за навчальним матеріалом уроку, так і узагальнюючі – за опорними задачами з певних тем, наприклад, опорні задачі трапеції, метод площ тощо (посібник Апостолової  Г.В., Ясінського В.В. «Планіметрія й стереометрія в опорних схемах і прикладах. Готуємося до ЗНО»).

З метою розвитку пошукових здібностей учнів запропонуйте їм сформулювати власні задачі, наприклад додаткові ознаки  рівнобедреного, прямокутного трикутників, паралелограма або трапеції (при повторенні відповідного матеріалу) тощо.

Однією з складностей сприйняття  матеріалу на уроці геометрії –  необхідність учневі виділити логічні кроки у розповіді вчителя, розставити акценти на елементах інформації і уявити їх у вигляді логічної схеми доведення. Тобто потрібно мовну (вербальну) інформацію вміти "перекладати" у логічну модель доведення. Треба вміти і навпаки – за математичною моделлю доведення  відновити його вербальний опис. Можна сказати, що це є вимогами щодо формування культури математичного мовлення в учнів, як писемного, так і усного. Такі вміння відразу не з’являються. І тут за особливостями сприйняття інформації можна виділити два типи учнів.

 Перший тип – "практик", тобто учень в якого сильною стороною є наочно-образна форма мислення. Таким дітям важко засвоювати знання, що подаються у вербальній формі, бо важко відобразити у слові процес розв’язання задачі. Вони можуть проявляти кмітливість при роботі з конкретним завданням, навіть отримати правильну відповідь, але коли вчитель викличе такого учня до дошки – він пояснити своє розв’язання не може. Такі діти можуть легко відтворювати складні конструкції, але мають проблеми у  мовному опису своїх конструкцій. Учні-практики важко засвоюють знання, коли вони позбавлені опори на конкретний наочний образ, на чітко і лаконічно сформовану логічну конструкцію.  Розвиток мовної сторони знань таких учнів повинен спиратись на їхню сильну сторону – наочно-образне мислення. Якщо надати можливість  таким учням (зазвичай то є хлопчики) засвоювати опорні знання у вигляді лаконічної моделі, дозволяти малювати блок-схему розв’язань, використовувати символіку теорії множин, навіть ввести якісь певні умовні позначення, не вимагаючи на перших кроках ідеального мовного відтворення думок, то через деякий час, після накопичення мовного досвіду   він "заговорить" і зможе переводити блок-схеми своїх розв’язань на прийняти мовне оформлення.  Але так відбувається лише в випадку коли дитина  накопичує практичний досвід власної  діяльності (розв’язує задачі), чує відповідні слова, вирази, фрази (мова вчителя) і в нього відбувається розвиток мислення, пам’яті, уваги. Якщо домінуючу роль у поданні інформації та при оцінюванні знань грає вербальна форма, то  учні-практики мають низькі оцінки і самооцінку, формується чекання неуспіху, зникає бажання вчитися, що, в свою чергу, стимулює ще більше відставання у навчанні. Більш того, чим старшим стає учень, тим важче йому поповнювати і без того малий запас абстрактних понять, які спираються як на фактичні, так і на мовні знання. Йде відставання не тільки в оволодінні навчальним матеріалом, але й у розвитку уваги, пам’яті, інших видів мислення.

Другий тип – "мовники", учні які легко сприймають вербальну інформацію, легко її відтворюють (зазвичай то дівчинки). Навчаються вони геометрії, як літературі та історії   – запам’ятовують події, вислови, фрази і легко повторюють їх на уроці. Їхні роботи з математики нагадують переказ підручника "близько до тексту". Але самостійно розв’язати нетипову задачу, або лаконічно і чітко сформувати логічну схему доведення для них є проблемою. Вони також потребують допомоги щодо розвитку – розвитку логічного та алгоритмічного мислення, але їхнє відставання у навчанні не так помітне, як в учнів-практиків.

Використання опорних конспектів (ОК) при навчанні геометрії допомагає  учням-практикам засвоїти навчальний матеріал, а учням-мовникам у вербальному поданні  матеріалу виділити головне, побачити логічну конструкцію доведення.

ОК полегшує як первинне сприйняття учнем матеріалу, так і його повторення. Рекомендується залучати до роботи одночасно з ОК у плакатах ще й альбоми з цими ж ОК, які має кожний учень. Тоді   поліпшується концентрація уваги дітей (не треба робити дві справи одночасно – писати і слухати) і зберігається час на уроці для розв’язання задач, полегшується засвоєння матеріалу – вмикається зорова  пам’ять, асоціативні зв’язки.

Після пояснення навчального матеріалу за ОК вчитель може на наступному уроці проговорити відповідний ОК за плакатом (2-3 хвилини) і звернути увагу на найбільш складні для учнів позиції ще раз. При тому він буде розповідати за тими самим малюнками і позначеннями, які використовував раніше, у тій самій послідовності – спрацюють асоціативні зв’язки, що сприятиме фіксації відповідної інформації у пам'яті учнів.

ОК допомагає виділити те головне, той цвях-опору на якому буде закріплено мінімум знань. Зрозуміло, що новий матеріал буде засвоєний, якщо усвідомлюється у опорі на знання головного з попереднього матеріалу. Як дати учневі цей вихідний мінімум, щоб він був міцно закріплений у довгочасній пам’яті? Мабуть, усім очевидно, що це відсутність у поясненнях зайвої інформації, короткі повторення, відновлення головних ланцюжків, тобто саме того матеріалу, який повинен бути переведений у довгочасну пам’ять. Самостійно виділити головне при первинному сприйнятті нових знань дуже складно навіть для більш-менш підготовленої людини. Що ж говорити про учнів середнього ступеня школи? Чим слабкіший учень, тим більша кількість повторень потрібна для закріплення опорних знань. Робота за ОК дозволяє учню легко здійснювати необхідне йому повторення.

Окрім того, ОК тренують здібність довільного запам’ятовування, тобто такого, яке чиниться без спеціальних зусиль з боку учнів, бо робота за ОК формує здатність автоматично виділяти співвідношення між формою матеріалу та його змістом, логічну структуру тексту. В іншому випадку (при роботі за підручником) найчастіше запам’ятовування учнів спрямовано в першу чергу на форму матеріалу (наприклад на мовну форму) без належного проникнення у зміст.

Робота за опорними схемами відокремлює дві діяльності – формування моделі і мовний її опис. Це дозволяє зосередитися учням-практикам на "перекладі" логічної конструкції на вербальний її опис, а учням-мовникам навпаки. Для цього рекомендується окремо проводити письмовий контроль по ОК і окремо – усне промовляння конспекту, коли учні розповідають його дивлячись у свій альбом з відповідним зображенням.

Треба ще раз зазначити, що усне промовляння ОК за малюнком вчить дітей математичному мовленню, розширює спеціальний запас слів і виразів, логічних зв’язків і дуже важливе на первинному етапі навчання геометрії. Якщо спочатку це дуже клопітлива та громіздка у часі справа – вислухати усіх (і на уроці, і на перерві, і після уроків), то після того, як “заговорять” декілька учнів, задача спрощується, бо ті, що "заговорили" стають помічниками вчителя (наприклад, приймають у однокласників промовляння ОК на "залік"/ "незалік").

Коли «заговорить» весь клас  (зазвичай то кінець 7 класу) можна вербальний опис ОК опускати – якщо учні пишуть ОК, то зможуть й проговорити. Ви маєте велику економію начального часу у поданні теоретичного матеріалу та у контролі володіння ним учнями. Звільнений час маємо використати для розв’язування задач, зокрема й логічного характеру.

ІІ. ОПОРНІ ЗАДАЧІ  В КУРСІ ГЕОМЕТРІЇ 7 КЛАСУ.  

Застосування опорних задач при розв’язуванні задач підвищеної складності – один з основних прийомів, якому потрібно навчити учня.

Доведення твердження опорної задачі не повинно бути громіздким (2-3 логічних кроки). Тоді  такі задачі легко сприймаються та запам’ятовуються учнями. Зверніть увагу учнів, що доведення теореми можна забути, а доведення твердження опорної задачі – НІ!

На початку уроку час від часу пропонуйте учням самостійну роботу на 3-5 хв. по доведенню твердження таких задач.  Про те, які самі задачі буде винесено на самостійну роботу треба попередити учнів. Тоді, щоб встигнути за 3-5 хв. написати таку роботу, учню треба вдома кілька разів прописати відповідне доведення. Відповідні опорні факти, логічні кроки їх доведення фіксуються у довгостроковій пам’яті учнів. (Зробити то та отримати гарну оцінку нескладно, бо доведення  не громіздке.)

На допомогу учню, у класі може стояти папка, оформлена вчителем, з набором таких задач. Відповідні доведення мають бути оформлені  лаконічно, писемною математичною мовою, із виділенням логічних кроків, із застосуванням кольорів у малюнках (кольори, як вважають психологи,  сприяють виділенню певних об’єктів та запам’ятовуванню).

Наведемо приклад таких задач та їх застосування, продемонструємо як такі прості  задачі допомагають «побачити» розв’язання зовсім непростих задач.

О.З. -1. Бісектриса кута – вісь симетрії цього кута.

Задача 24. (Олімпіада - ІІІ етап. )  Відновити трикутник за прямими, що містять бісектриси його кутів і точкою перетину однієї з бісектрис зі стороною трикутника.

Нехай треба побудувати ΔАВС за прямими l_A, l_B, l_C , що містять бісектриси кутів А, В, С відповідно, і точкою Т перетину l_B зі стороною АС.

План побудови

1. Будуємо точки,  симетричні точці Т відносно l_A і l_C – маємо відповідно точки Т₁ і Т₂ (на сторонах АВ і ВС).
2. Будуємо точку симетричну Т₁ відносно  l_B – маємо точку Т₃ (на ВС).
3. Пряма  Т₃Т₂ перетинає  l_B, l_C у точках В і С.
4. пряма ТС перетинає l_A у точці А.

Трикутник АВС відновлено.

О.З. -2.  Бісектриса – ГМТ рівновіддалених від сторін кута.

О.З. -3.  У прямокутному трикутнику проти більшого з катетів міститься кут               більший за 45^о.

Задача 25. (Олімпіада –ІІІ ет.). У гострокутному трикутнику АВС: АD – бісектриса, ВМ – висота. Доведіть, що кут СМD більший за 45^о.

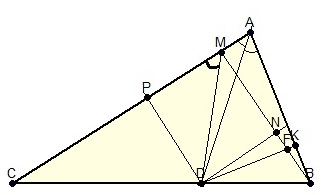
1. Точка D належить бісектрисі кута А, отже відстані DP і DK цієї точки до сторін АС і АВ трикутника рівні (О.З.-3).
2. Нехай DK перетинає ВМ у точці F. Проведемо DN ВМ. Маємо: PM = DN, як сторони прямокутника PМND.
3.  DN <DF, як катет і гіпотенуза трикутника DNF. Тоді DP = DK > DN = PM.
4. У прямокутному трикутнику MPD маємо DP  >  PM, тоді  . Звідки випливає правильність твердження задачі (О.З.-4).

ІІІ. ПІДХОДИМО ДО ПОНЯТТЯ ПРО ГРАФ

Задача 26. У першості з настільного тенісу беруть участь шість учасників: А, Б, В, Г, Д і О. Першість проводиться за круговою системою – кожний учасник грає з іншим лише один раз. Деякі ігри вже проведені: А зіграв з Б, Г і О; Б грав з А і Г; В – з Г, Д і О; Г – з А, В, Б; Д – з В; О – з А і В. Скільки ігор вже проведено і скільки ще залишилось провести?

Відповідь: 7 і 8 відповідно. Порада. Позначте точки А, Б, В, Г, Д і О так, щоб щодні 3 них не містилися на одній прямій. З’єднайте дві точки відрізком, якщо відповідна пара грала. Підрахуйте кількість утворених відрізків – їх 7. Іншим кольором або пунктиром зобразіть відрізки з кінцями в даних точках, які ще не було на малюнку – їх 8.

Математики називають графом множину точок та таких відрізків, обидва кінці яких належать точкам вказаної множини. Ці точки називають вершинами графа, а відрізки – ребрами графа.

Граф називається зв’язним, якщо рухаючись уздовж його ребер, можна з будь – якої його вершини потрапити у будь-яку іншу.  Начебто, просте поняття зв’язності графа дозволяє легко розв’язувати не прості (з першого погляду) задачі.

Задача 27. На деякому острові 15 поселень, кожне з яких з’єднано шляхом не менше, ніж з 7 іншими. Доведіть, що з будь – якого поселення цього острова можна добратися шляхами до будь – якого іншого. (Можна проходити через інші поселення.)

Розв’язання.

Нехай існують два такі поселення, що з одного не можна добратися до іншого, якщо йти шляхами цього острова. Тоді відповідний граф має вигляд, який представлено на малюнку 22. 11. Таким чином, маємо не менш як 16 поселень, що суперечить умові.

ІV. НА ЗАКІНЧЕННЯ

Задача 28.  Двоє гравців по черзі кладуть квасолини у клітинки таблиці розміром 9  9. За один хід можна покласти одну квасолину в будь – яку клітинку. Виграє той, хто покладе останню квасолину. Хто переможе?

Джерело

http://www.академія.com.ua/archives/2802

20 жовтня 2015 року вебінаром з теми “Створення інтерактивних модулів з математики за допомогою інтернет-ресурсу Learningapps” розпочалися заняття обласної школи передового педагогічного досвіду Гартфіль Олександри Романівни, Показій Антоніни Петрівни, вчителів математики Макарівського навчально-виховного комплексу “Загальноосвітня школа І-ІІІ ступенів – природничо-математичний ліцей”, вчителів-методистів, з проблеми “Використання засобів інформаційно-комунікаційних технологій на уроках математики” в 2015-2016 н.р.

Актуальність цього вебінару продиктована тим, що все більше вчителів використовують  у навчальному процесі електронні дидактичні матеріали. В сервісі Learningapps можна використовувати як готові інтерактивні вправи, так і створювати свої на основі шаблонів.

Переглянути запис вебінару за посиланням http://www.wiziq.com/online-class/3203885-створення-інтерактивних-модулів-за-допомогою-сервісу-learning-apps

Зареєструватися на https://learningapps.org/